Wilkinson Leistungsteiler mit Diskreten Bauteilen

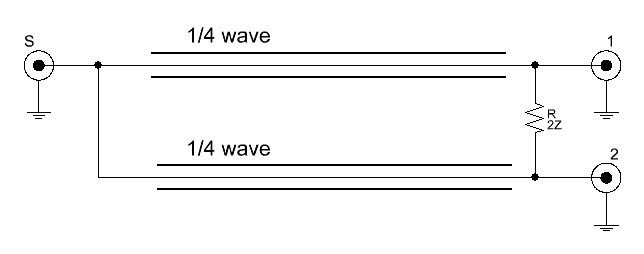
Für dieses Beispiel seien folgende Designparameter gegeben: Ein Wilkinson-Teiler soll ein Signal bei 28 MHz auf zwei verschiedene Lasten verteilen. Die Systemimpedanz beträgt 50 Ohm. Zunächst ein kurzer Blick auf das grundsätzliche Design eines Wilkinson-Teilers basierend auf einem λ/4-Leitungstransformator:

Klassischer Wilkinson-Teiler mit λ/4-Leitungstransformator

Der Aufbau ist sehr simpel: Die hohe Isolation zwischen Port 1 und 2 kommt dadurch zustande, dass ein periodisches Signal durch den Widerstand R seinen historischen, um 180° phasenverschobenen Spiegel begegnet. Das liegt daran, dass die Laufzeit durch zwei mal λ/4 lange Leiter einen Phasenunterschied von 180° zum Ursprungssignal aufweist. Der Widerstand ist so zu dimensionieren, dass er doppelt so hoch ist, wie die Systemimpedanz. Bei 50 Ohm Systemen also 100 Ohm.

Die Impedanz des λ/4 Leiters ist mit der Wurzel aus 2 multipliziert mit der Systemimpedanz zu bemessen. Für 50 Ohm Systeme entspricht dies einer Impedanz von 70.7 Ohm.

Jetzt benötigt man nur noch zwei Leiter mit der exakten, elektrischen Länge einer viertel Wellenlänge (λ/4) bezogen auf die Betriebsfrequenz. Dabei ist der Verkürzungsfaktor für das verwendete Material zu berücksichtigen. Kennt man die Dielektrizitätskonstante des verwendeten Materials, ist die Berechnung sehr leicht. Hierzu gibt selbstverständlich auch kostenlose Software, beispielsweise AppCAD [1]. Für Rogers 4003 material, sieht die Simulation beispielsweise wie folgt aus:

Microstrip line calculation in AppCAD

Ein Leiter mit der Länge λ/4 bei 28 MHz auf Rogers 4003 Material müsste also rund 1,65 Meter lang sein! Auch wenn die Kosten für Leiterplatten heutzutage sehr gering sind, ist so ein Design natürlich nicht sonderlich platzsparend. Wäre es nicht schön, wenn es eine Ersatzschaltung gebe, die in Punkto Impedanz und Phasenlaufzeit die gleichen Eigenschaften besitzt, wie ein λ/4-Transformator? Ein Pi-Filter aus diskreten Bauteilen ist hierfür genau der richtige Kandidat. Pi-Filter können so bemessen werden, dass sie sich elektrisch exakt wie λ/4-Transformatoren verhalten.

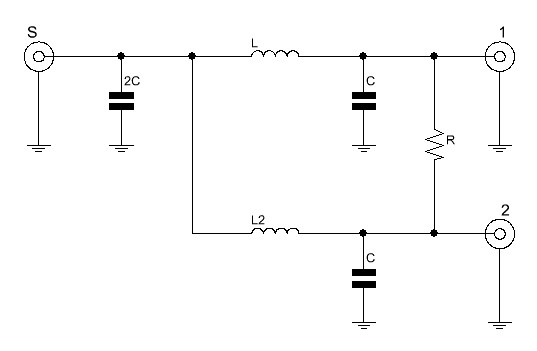
Tauscht man im oben gezeigter Grundschaltung die λ/4-Transformatoren durch je einen Pi-Filter, erhält man folgendes Schaltbild:

Wilkinson Teiler mit diskreten Bauelementen

R ist weiterhin mit der zweifachen Systemimpedanz zu bemessen. In diesem Fall also weiterhin 100 Ohm. Die Reaktanz von C und L sind gleich der Impedanz, die ein Leiter mit der Länge λ/4 laut der oben angegebenen Formel haben müsste. In 50 Ohm Systemen also 70,7 Ohm. Mit dieser Information lassen sich die benötigten Induktivitäten und Kapazitäten berechnen:

Das ist nah genug an 400 nH, dass ich es dahingehend abrunde. Vor Allem auch aus dem Grund, dass ich zufällig gerade keine 401,92 nH Spulen auf Lager habe. 400 nH wird da deutlich einfacher zu finden sein. Als nächstes werden nun die zu den 400 nH Spulen passenden Kondensatoren berechnet.

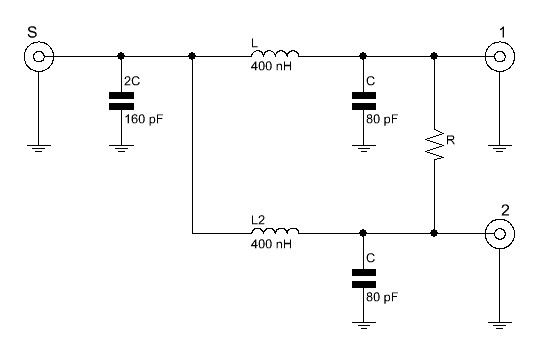
Das Ergebnis wird ebenfalls auf 80 pF abgerundet. Alle mit „C“ bezeichneten Kondensatoren müssen also mit 80 pF bemessen sein. Der mit „2C“ bezeichnete Kondensator Summen-Port (S) hat die doppelte Kapazität, in diesem Fall also 160 pF. Es spricht natürlich überhaupt nichts dagegen tatsächlich zwei 80 pF Kondensatoren am S-Port zu verwenden. Das fertige Design sieht entsprechend wie folgt aus:

Wilkinson-Teiler für eine Betriebsfrequenz von 28 MHz

So leicht lässt sich ein Wilkinson-Teiler berechnen. In der Praxis hilft es oft errechnete Bauteilewerte eher ab- anstatt aufzurunden. Das liegt daran, dass parasitäre Kapazitäten und Induktivitäten die Betriebsfrequenz tendenziell eher nach unten verschieben. Durch abrunden der Bauteile lässt sich dieser Effekt zumindest etwas eindämmen.

Fertig aufgebauter Wilkinson-Teiler für eine Betriebsfrequenz von 28 MHz

Links and Sources:

[1] AppCAD: https://www.broadcom.com/appcad