Impedanzanpassung mit dem L-Netzwerk

Impedanzanpassung ist eine allgegenwärtiges Herausforderung für Hochfrequenzschaltungen. Das L-Netzwerk ist eine einfache, verlustarme Methode um unterschiedliche Impedanzen aneinander anzupassen. Dieser Artikel soll zeigen wie man ein passendes L-Netzwerk für komplexe Impedanzen berechnet.

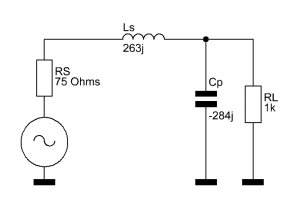
Die niedrige Ausgangsimpedanz eines Leistungs-MOSFET an eine höhere Systemimpedanz, beispielsweise 50 oder 75 Ohm, anzupassen ist ein typisches Problem in der Entwicklung von Hochfrequenzschaltungen. Für diesen Artikel passen wir den 75 Ohm Ausgangswiderstand eines Funktionsgenerators an eine 1000 Ω Lastimpedanz bei einer Frequenz von 16 MHz an.

Um die Funktionsweise eines L-Netzwerkes zu erklären, präsentiere ich erst das fertige Netzwerk, erkläre die Funktionsweise und erst danach erkläre ich die Berechnung der einzelnen Komponenten.

RS = Quellwiderstand (75 Ohm)
RL = Lastwiderstand (1000 Ohm)
Ls = Serien-Induktivität (j263)
Cp = Parallel-Kapazität (-j284)

Das kleine „j“ wirkt erstmal etwas befremdlich. Zumindest, wenn man es noch nie zuvor gesehen hat. Das „j“ steht in der Elektrotechnik für die imaginären Einheit i. Da in der Elektrotechnik das kleine „i“ bereits anderweitig belegt ist, hat man sich für die Verwendung von „j“ entschieden. Ein positiver Wert zeigt eine induktive Reaktanz, ein negativer Wert eine kapazitive Reaktanz an. Im Prinzip heißt es nicht Anderes, als dass wir eine Spule (Ls) mit einer Reaktanz von 263 Ohm und einen Kondensator (Cp) mit einer Reaktanz von 284 Ohm verwenden. Da diese Reaktanzen abhängig von der Signalfrequenz sind, ist ein L-Netzwerk nicht sonderlich breitbandig.

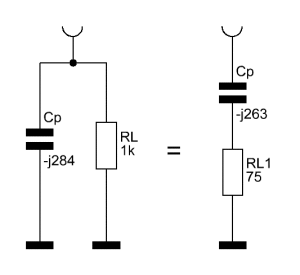
Wie schafft es diese Schaltung nun eine 1000 Ohm Last wie 75 Ohm auszusehen und andersrum? Um diese Frage zu beantworten kommen wir um ein wenig Mathematik nicht herum. Fangen wir mit RL und Cp an. Die beiden sind parallel geschaltet. Die daraus resultierende Impedanz errechnet sich wie folgt:

75 Ohm ist der resistive Anteil an der resultierenden komplexen Impedanz, 263 Ohm der reaktive (kapazitive) Anteil. Das heißt, dass die Parallelschaltung von RL und Cp sich so benimmt als sei ein 75 Ohm Widerstand mit einem Kondensator mit 263 Ohm Reaktanz in Serie geschaltet. Man nennt dies auch die äquivalente Serienimpedanz.

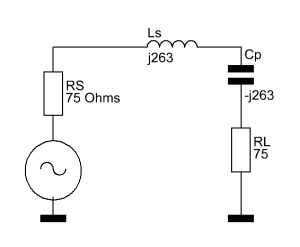
Wenn wir diese soeben berechnete äquivalente Serienimpedanz nun in das ursprüngliche L-Netzwerk einbauen, erhalten wir folgendes Ersatzschaltbild:

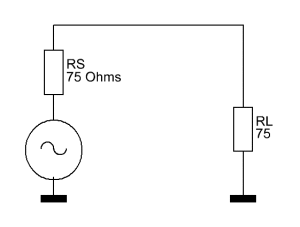
Es fällt auf, dass die Serieninduktivität Ls und der äquivalente Serienkondensator nun betragsmäßig die gleiche Reaktanz haben, wenngleich auch mit unterschiedlichen Vorzeichen. Diese beiden Reaktanzen heben sich nun einfach gegenseitig auf. Der Lastwiderstand von 1000 Ohm sieht für den Signalgenerator nun aus wie ein 75 Ohm Widerstand.

Ein praktischer Nebeneffekt eines solchen L-Netzwerkes ist, dass es eine Tiefpasscharakteristik hat. Beispielsweise beim Anpassen einer LDMOS Endstufe an eine Systemimpedanz von 50 Ohm ist dieser Effekt von Vorteil um Obertonaussendungen zu unterdrücken. Eine Hochpasscharakteristik lässt sich mit einem L-Netzwerk auch realisieren, wenn man die Positionen von Ls und Cp tauscht. An der prinzipiellen Funktionsweise eines L-Netzwerkes würde dies nichts ändern, jedoch müssen die Werte neu berechnet werden.

Wie berechnet man so ein L-Netzwerk nun von Anfang an? Wir nehmen unser Beispiel mit 75 Ohm Quellwiderstand, 1000 Ohm Lastwiderstand und einer Betriebsfrequenz von 16 MHz. Zuerst muss die Kreisgüte, auch Q-Faktor genannt, berechnet werden.

R_Last = Lastwiderstand
R_Quelle = Quellwiderstand

Mit dem berechneten Q-Faktor von 3,512 können wir nun die Reaktanz der Induktivität berechnen.

Die verwendete Induktivität soll also eine Reaktanz von 263 Ohm bei 16 MHz haben. Die 263 Ohm können und sollten wir wieder als j263 schreiben um zu unterstreichen, dass es sich hier um eine induktive Reaktanz handelt.

Um die benötigte Reaktanz des Kondensators Cp zu errechnen, wird der Lastwiderstand durch den Q-Faktor geteilt.

Der Kondensator Cp sollte also eine Impedanz von 284 Ohm bei 16 MHz haben. Auch hier können wir das Ergebnis als -j284 schreiben um auf die kapazitive Natur der Reaktanz hinzuweisen.

Zuletzt müssen die errechneten Werte noch in eine konkrete Induktivität und Kapazität bei 16 MHz umgewandelt werden.

Die Induktivität sollte also 2,6 μH betragen. Der nächstübliche, käufliche Wert wäre 2,2 μH. Da in der Realität ohnehin ausreichend parasitäre Induktivität in der Schaltung vorhanden sein wird, rechnen wir einfach mit 2,2 μH weiter. Als nächstes wird der Kondensator berechnet:

Der verwendete Kondensator Cp sollte also eine Kapazität von 35 pF haben. Auch hier habe ich einfach den nächsten Normwert von 33 pF verwendet. Um die Funktion des Berechneten L-Netzwerkes zu überprüfen, habe ich die Rückflussdämpfung mit einer Messbrücke gemessen. Der Signalgenerator wurde auf eine Ausgangsimpedanz von 75 Ohm eingestellt. Die Messkabel vom Signalgenerator zur Messbrücke und von der Messbrücke zum Oszilloskop, sowie die Messbrücke selbst, sind ebenfalls für eine Systemimpedanz von 75 Ohm ausgelegt.

Ergebnis: Die Schaltung funktioniert exakt so, wie sie soll. Die beste Impedanzanpassung hat diese Schaltung bei 16,1 MHz erbracht. Ein bisschen Abweichung von den Berechnungen war zu erwarten. Vor Allem auch, weil die Bauteilewerte auf die nächsten Normwerte gerundet wurden.