Löschfunkensender Selbstgebaut

Dieser Artikel bietet einen interessanten Einblick in die faszinierende Welt der frühen Funktechnologie, die einst die globale Kommunikation revolutionierte. Durch den Aufbau und die Analyse eines Löchfunkensenders bietet dieses Projekt einen praktischen Einblick in die faszinierenden Dynamiken gedämpfter harmonischer Oszillatoren und erläutert Merkmale wie das logarithmische Dekrement, die Abklingrate, den Dämpfungsfaktor, den Q-Faktor und vieles mehr.

Einfacher Löschfunkensender aufgebaut aus wenigen Komponenten auf etwas Acrylglas

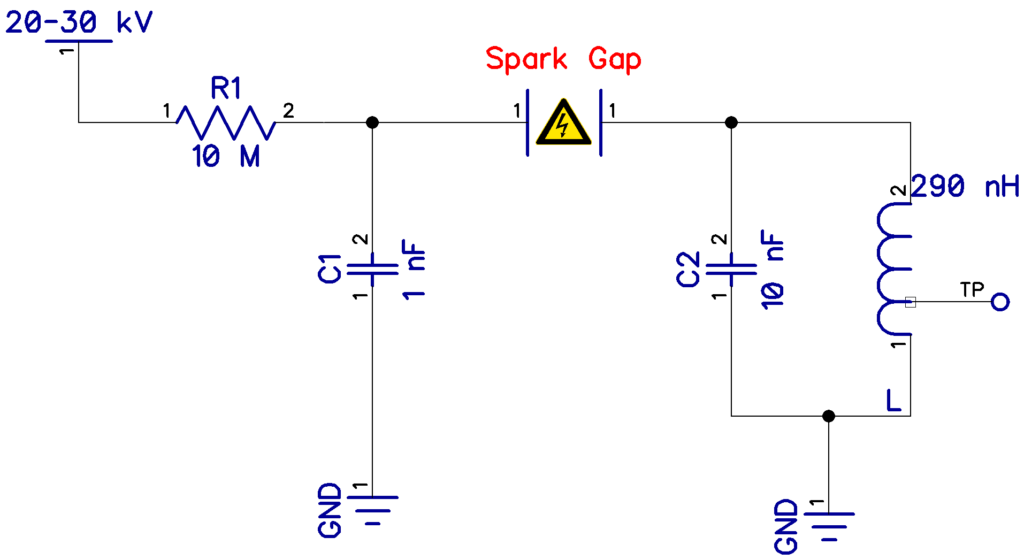
Schaltung

Die grundlegende Schaltung für einen Löschfunkensender ist sehr übersichtlich. Es soll allerdings angemerkt werden, dass die hier gezeigte Schaltung wenig mit tatsächlich eingesetzten Schaltungsvarianten zu tun hat. Dennoch sind die grundlegenden Prinzipien gleich und erfüllt seinen Zweck als Anschauungsobjekt.

Einfacher Löschfunkensender mit einer Sendefrequenz von rund 3 MHz.

Die Funkenstrecke selbst besteht aus zwei Schlossschrauben und etwas Acrylglas. Die Durchbruchspannung von Luft ist ca. 3 kV/mm, zumindest wenn man ein idealisiert homogenes Feld und einen Elektrodenabstand von 10 mm annimmt. Zwar vernachlässigt diese Annahme ein wenig Realität. Für den hier gezeigten Zweck ist dies allerdings völlig ausreichend und ein Exkurs in das Paschen-Gesetz wäre über das Ziel hinausgeschossen. Die aufgebaute Funkenstrecke hat eine Durchbruchspannung von ca. 18 kV, entsprechend einem Elektrodenabstand von 6 mm.

Die Feuerrate der Funkenstrecke wird durch das Zeitglied bestehend aus C1 und R1 bestimmt. Der Spannungsverlauf an C1 folgt der Gleichung 1. Hierbei ist _C1 die Spannung an C1, U_in die Eingangsspannung an R1 und t steht für die Zeit seit Anlegen der Betriebsspannung (oder dem letzten Funkenüberschlag) in Sekunden. Als Faustregel kann gesagt werden, dass nach einer Zeitkonstante (R1 mal R2) die Spannung an C1 ca. 63% der angelegten Betriebsspannung beträgt. Dieser wert steigt auf ca. 87% nach insgesamt zwei Zeitkonstanten. Daher bietet dieses einfache RC Zeitglied einen einfachen Weg die Überschlagshäufigkeit der Funkenstrecke zu kontrollieren. Diese Eigenschaft ist deshalb interessant, weil die Überschlagshäufigkeit direkt die Tonhöhe des ausgesandten Signales in einem AM-Empfänger bestimmt.

(1) $\begin{equation*} U_{C1} = U_{in} (1 - e^{\frac{-t}{R_1 C_1}}) \end{equation*}$

Sobald die Durchbruchspannung erreicht ist, schlägt der Funken in der Funkenstrecke über. Dadurch entsteht ein niederohmiger Pfad, der einen Ladungsausgleich zwischen C1 und C2 ermöglicht und damit den Schwingkreis, bestehend aus C2 und L1, anregt. Die Resonanzfrequenz wird folglich hauptsächlich von C2 und L1 bestimmt (Gl. 2). Diese Annahme ist zumindest weitestgehend wahr, vernachlässigt allerdings zunächst den (in diesem Fall störenden) Einfluss von C1. Hierzu allerdings später mehr. Mit den hier gezeigten Bauteilewerten beträgt die Resonanzfrequenz ungefähr 3 MHz (Gl. 3).

(2) $\begin{equation*} f_r = \frac{1}{2 \pi \sqrt{LC}} \end{equation*}$

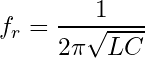
(3) $\begin{equation*} f_r = \frac{1}{2 \pi \sqrt{290\;nH \cdot 10\;nF}} = 2,95543\;MHz \end{equation*}$

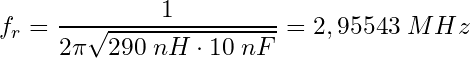
Die in der Schaltung verwendeten Bauteile müssen natürlich über die notwendige Spannungsfestigkeit verfügen. R1, C1 und C2 haben eine Spannungsfestigkeit von über 30 kV. L1 ist eine aus Kupflerlackdraht selbst gewickelte Luftspule mit einem Durchmesser von 8mm und 8 Windungen. Die Spule verfügt über eine Anzapfung 1,5 Windungen von der Masseseite zur niederohmigen Auskopplung des generierten Signales. An dieser Stelle soll noch angemerkt werden, dass der Einsatz von Löschfunkensendern für tatsächliche, drahtlose Kommunikationsanwendungen in den meisten Ländern der Welt verboten ist. Dies liegt an der extrem breitbandigen Natur des generierten Ausgangssignales.

Test und Analyse

Für einen ersten Test wird eine kurze Drahtantenne, bestehend aus wenigen Metern 1,5mm² Litze direkt an die Anzapfung an Spule L1 gelötet. Der Löschfunkensender wird von meinem selbstgebauten 30 kV Hochspannungsnetzteil versorgt.

Das demodulierte Signal wurde mehrfach mit verschiedenen Versorgungsspannungen und Empfängern aufgenommen. Einmal mit einem SDRplay RSPdx / SDRuno und ein weiteres mal mit einem XHDATA D-808:

Als nächstes wird der Antennendraht entfernt und ein Oszilloskop-Tastkopf angeschlossen. Um die Zerstörung meiner besseren Oszilloskope zu vermeiden, wird hierfür ein günstigeres Oszilloskop verwendet. Daher entschuldige ich mich im Voraus für die geringe Auflösung der Screenshots. Das Oszilloskop wird auf Einzelaufnahme gestellt und die Hochspannung kurz angelegt um einen Impuls der Ausgangswellenform aufzunehmen.

Testaufbau: Hochspannungsnetzteil (Rechts), Löschfunkensender (Mitte) und Oszilloskop (Links)

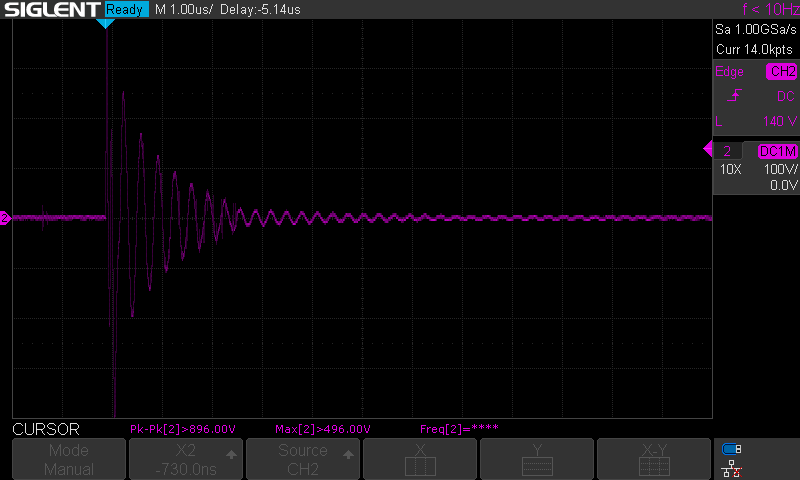
Am Ausgang ist ein sinusförmiges Signal mit einer schnell abklingenden Amplitude ist klar erkennbar. Die Frequenz liegt um ca. 3 MHz. Aufmerksamen Lesern mag auffallen, dass die ersten 1,5 Perioden des Signales eine deutlich höhere Frequenz haben. Dieser Teil wird zunächst ignoriert und die Ursache später erneut aufgegriffen. Bei der aufgenommenen Wellenform handelt es sich um einen einzelnen Ausgangsimpuls, der sich mit der Feuerrate der Funkenstrecke wiederholt.

Ausgangswellenform eines einzelnen Impulses des Löschfunkensenders.

Es benötigt wenig Kreativität um zu erkennen, dass die Hüllkurve der Amplitude einer logarithmischen Abklingrate folgt. Dieses Verhalten ist typisch für gedämpfte, harmonische Oszillatoren aller Art (Federpendel, Drehschwinger, Schwingkreise, etc.). Daher haben sich umfangreiche, mathematische Methoden etabliert, die das Verhalten einer solchen Oszillation beschreiben können. Das Schwingungsverhalten kann durch die Gleichung 4 beschrieben werden. Mit der Ausgangsspannung u(t) zum Zeitpunkt t, û dem Spitzenwert zum Zeitpunkt t=0, der Abklingkonstante δ und der Kreisfrequenz ω =2πf. Die einzelnen Parameter des Löschfunkensenders werden nun ermittelt und hieraus eine Schwingungsgleichung entwickelt.

(4) $\begin{equation*} u(t) = \hat{u} e^{- \delta t} \cos(\omega t) \end{equation*}$

Ausgangsimpuls eines Löschfunkensenders

Mit Hilfe der Markerfunktionen und weiterem Ignorieren der ersten 1,5 Perioden, kann die Frequenz von rund 3 MHz bestätigt werden. Ganz genau sind es 2,976 MHz. Der Spitzenwert der ersten Periode ist 266 V, der zweiten Periode 174 V. Die folgenden Spitzenwerte betragen 126 V, 96 V und 52 V. Mit Hilfe dieser Informationen wird zunächst das logarithmisches Dekrement Λ (Lambda) berechnet (Gleichungen 5 und 6).

(5) $\begin{equation*} \Lambda = \frac{1}{n} \ln(\frac{A}{A_n}) \end{equation*}$

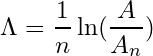
(6) $\begin{equation*} \Lambda = \frac{1}{6} \ln(\frac{266\;V}{52\;V}) \approx 0,272 \end{equation*}$

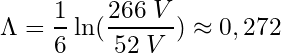
Das logarithmisches Dekrement wird nun durch die Periodendauer (1/f) dividiert um die Abklingrate δ (Delta) zu errechnen (Gleichungen 7 und 8).

(7) $\begin{equation*} \delta = \frac{\Lambda}{T_d} \end{equation*}$

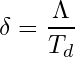
(8) $\begin{equation*} \delta = \frac{0,272}{3,36\; \cdot 10^{-7}} \approx 8,1 \cdot 10^5 \end{equation*}$

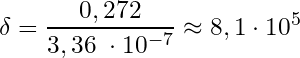
Aus den berechneten Werten lässt sich nun durch Einsetzen in 4 direkt eine Schwingungsgleichung für das Ausgangssignal des Löschfunkensenders aufstellen (Gl. 9).

(9) $\begin{equation*} u(t) = 266\;V\;e^{-8,1 \cdot 10^5\;t} \cos(2\;\pi\;2,976\cdot 10^6\;t) \end{equation*}$

Die Aufgestellte Schwingungsgleichung wird mit Hilfe von Python graphisch dargestellt und das Ergebnis mit dem gemessenen Ausgangssignal verglichen.

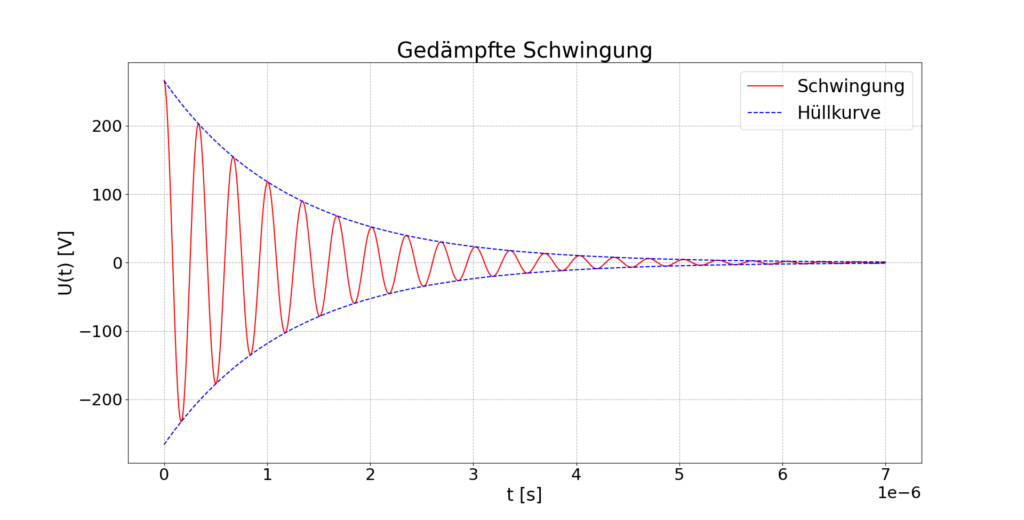
Errechnete Simulation der Ausgangsspannung u(t) mit Hilfe von Python und der aufgestellten Schwingungsgleichung

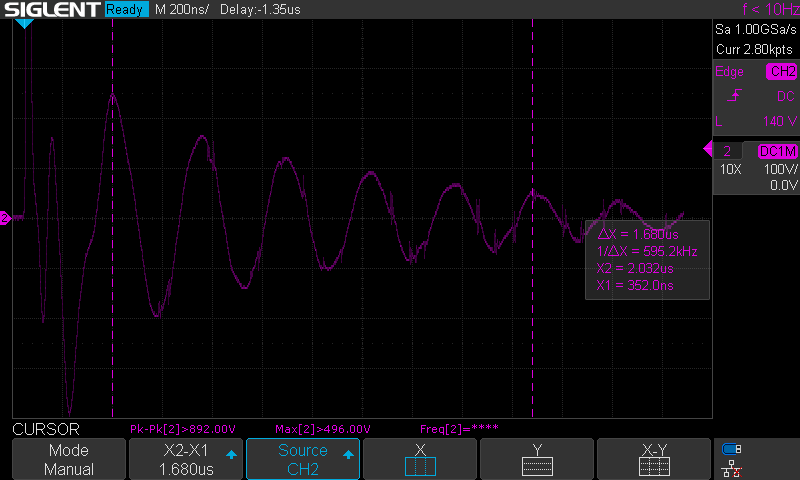
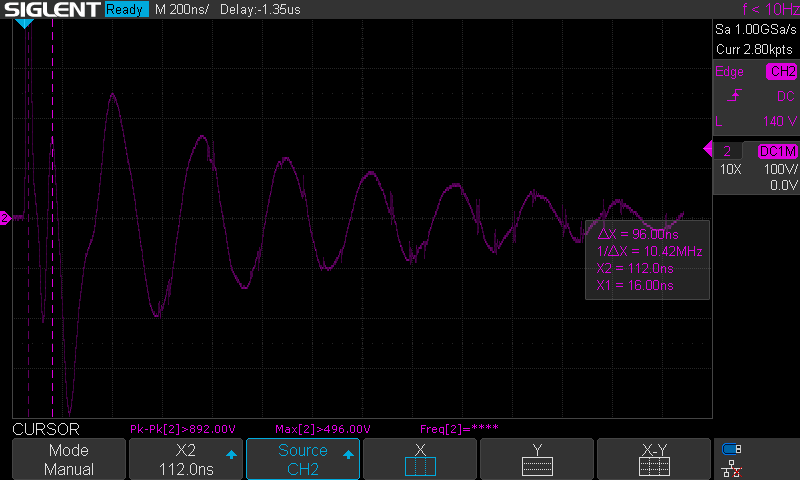
Das Schwingungsverhalten und die Hüllkurve der Amplitude sieht dem messtechnisch erfassten Signal sehr ähnlich. Im gemessenen Signal ist allerdings eine soweit nicht beachtete, höherfrequente Schwingung am Anfang des Ausgangsimpulses vorhanden. Unter Verwendung der Markerfunktion kann die Frequenz dieser Oszillation mit 10,42 MHz bestimmt werden.

10,42 MHz Oszillation am Anfang des Ausgangsimpulses

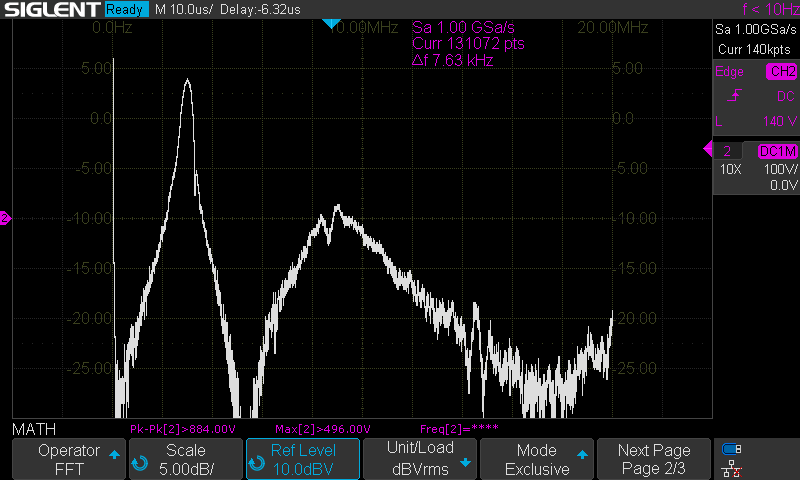
10,42 MHz sind ungefähr das 3,33-fache der gewünschten Ausgangsfrequenz. Unter der Annahme, dass L1 konstant ist, entspricht dies unter Anwendung von Gleichung 2 einer Parallelkapazität von 1 nF. Dies entspricht wenig zufällig exakt der Dimensionierung von C1. In dem Moment, wo die Funkenstrecke überschlägt, ist C1 geladen und C2 entladen. Zwar beginnt der Ladungsausgleich zwischen C1 und C2 quasi sofort, für einen kurzen Moment interagieren C1 und L1 allerdings unter Auslassung von C2 miteinander. Dies ist die Ursache für die höherfrequente Schwingung am Anfang eines jeden Ausgangpulses. Dieses Phänomen zeigt sich auch deutlich im Ausgangsspektrum.

Ausgangsspektrum des Löschfunkensenders

Das Ausgangsspektrum sieht in Bezug auf elektromagnetische Verträglichkeit aus, wie ein düsterer Alptraum. Die Bandbreite steht in keinem gute Verhältnis zum Nachrichtengehalt. An einer resonanten Antenne wäre das abgestrahlte Spektrum natürlich etwas schmalbandiger, allerdings immer noch sehr verschwenderisch. Apropos Bandbreite: Aus dem zuvor berechneten lograrithmischen Dekrement lässt sich mit einem Umweg über den Dämpfungsfaktor D auch der Gütefaktor Q, auch Q-Faktor genannt, berechnen (Gl. 10 und 12).

(10) $\begin{equation*} D = \frac{\Lambda}{\sqrt{(2 \pi)^2 + \Lambda^2}} \end{equation*}$

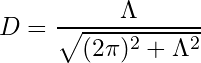
(11) $\begin{equation*} D = \frac{0.272}{\sqrt{(2 \pi)^2 + 0.272^2}} \approx 0,04324 \end{equation*}$

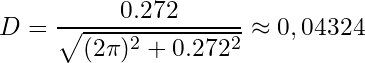
(12) $\begin{equation*} Q = \frac{1}{2 D} \end{equation*}$

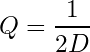
(13) $\begin{equation*} Q = \frac{1}{2\cdot0.04324} \approx 11,56 \end{equation*}$

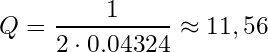
Der rechnerische Gütefaktor beträgt 11,56 (Gl. 10 und 13). Bei einer Frequenz von 3 MHz entspricht eine Güte von 11,56 einer Halbwertsbandbreite von rund 260 kHz. Dies deckt sich ungefähr mit dem gemessenen Ausgangsspektrum.

Video

Ein Bild sagt mehr als tausend Worte. Ein Video sagt folglich mehr als eine Million Worte. Daher habe ich die hier behandelten Inhalte in einem Video aufbereitet:

Links and Sources:

[1] „Einstellbares 30 kV Hochspannungs-Netzeil im Eigenbau“, Baltic Labor: https://baltic-labor.de/

Bitte zitieren als:
S. Westerhold: Löschfunkensender Selbstgebaut (2024), in: Baltic Labor Blog für Hochfrequenz- und Messtechnik, ISSN (Online): 2751-806X, URL: https://baltic-labor.de/2024/04/loeschfunkensender-selbstgebaut/ (Stand: 21.11.2024).

Schaltung

Test und Analyse

Video

Leave a comment Antworten abbrechen