Stereo-Multiplexsignal mit einem Funktionsgenerator und Python erzeugen

Die Art und Weise, wie ein FM-Stereo-Signal kodiert wird ist simpel und ausgeklügelt zugleich. Zunächst wird aus den rechten und linken Audiosignal ein Summensignal gebildet. Das Summensignal stellt eine Rückwärtskompabilität mit älteren Mono-Empfängern sicher. Weiter wird ein Differenzsignal aus den beiden Audio-Signalen gebildet. Dieses Differenzsignal wird verwendet um ein Doppelseitenband-Signal um eine Mittenfrequenz von 38 kHz zu erzeugen. Zuletzt wird ein zu dem 38 kHz phasenkohärenter 19 kHz Pilotton mit einer relativen Amplitude von 10 % zu den beiden vorhergenannten Signalen hinzugefügt. Diese drei Signale werden zusammen verwendet um einen FM-Sender zu modulieren. Für eine ausführlichere Erklärung verweise ich auf mein YouTube-Video zur Stereo-FM Theorie [1](EN).

Für das Testsignal sollte das MPX-Signal einen 700 Hz Ton im linken Audiokanal und einen 2200 Ton im rechten Audiokanal enthalten. Als Funktionsgenerator wurde ein Siglent 1032X verwendet. Auf Softwareseite wurde Python mit PyVISA und NI-VISA verwendet. Letztere bieten eine einfache Methode um mit modernen Laborgeräten zu kommunizieren.

Stereo-Multiplexsignal mit SDG1032X and Python erzeugen

The first step was to figure out how to generate the necessary datapoints for the MPX signal. In order to achieve this, equations describing all components of the final signal in a mathematical form needed to be formulated. For the sum signal, the DSB modulated difference signal and the 19 kHz pilot tone, the equations are as follows:

Als ersten Schritt galt es die Datenpunkte für die gewünschte Stereo-Multiplex-Wellenform zu erzeugen. Dazu wurden zunächst die Gleichungen für das Summensignal, das Doppelseitenbandsignal mit dem Differenzssignal und den 19 kHz Pilotton aufgestellt:

Gleichung für das Summensignal (L+R) signal:

Gleichung für das Differenzsignal (L-R), doppeltes Seitenband mit 38 kHz Träger:

Gleichung für den 19 kHz Pilotton:

Bei ω ahndelt es sich in diesem Fall um einen Normalisierungsfaktor um Frequenzen von Zyklen pro Sekunde in Radian pro Abtastwert zu übersetzen. Die Zeit zwischen den Abtastwerten wird durch den Buchstaben t repräsentiert. In der Python- / SDG-Kombination beträgt der Normalisierungsfaktor π geteilt durch die doppelte Abtastrate des SDG1032X. Da die drei generierten Signale einfach addiert werden, kann folgende Gesamtgleichung aufgestellt werden:

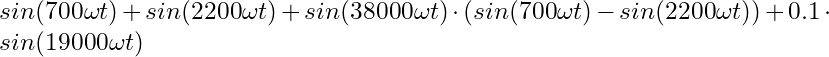
Die Gesamtgleichung erzeugt einen Maximalwert von 2,1 und einen Minimalwert von -2,1. Daher muss die Gleichung mit dem Faktor 0,47 multipliziert werden um einen Maximalwert von 1 bzw. einen Minimalwert von -1 zu erhalten.

Der vollständige Python-Code, zusammen mit anderen Python / PyVISA Beispiel-Skripten, kann über mein SIGLENT GitHub Repository [2] abgerufen werden.

Das Python-Skript muss 16384 Datenpunkte für die oben mathematisch beschriebene Wellenform generieren. Das folgende Python-Skript ist zwar nicht das hübscheste, es erledigt jedoch genau diese Aufgabe:

# Leeres Array mit 16384 Punkten erstellen
WAVE = np.arange(0, 0xfffe, 1);

  # Amplitude (MAX 32767 on SDG1032X)
  Amplitude = 32767
  WAVE[n] = 0.47*Amplitude*(np.sin(700*F_FACTOR*n)+np.sin(2200*F_FACTOR*n)+0.1*np.sin(19000*F_FACTOR*n)+np.sin(38000*F_FACTOR*n)*(np.sin(700*F_FACTOR*n)-np.sin(2200*F_FACTOR*n)))

Die so generierten Datenpunkte der Wellenform werden dann mit Hilfe des PyVISA-Packages und den notwendigen SCPI-Kommandos an den Funktionsgenerator gesendet. Dafür muss das PyVISA-Package und die NI-VISA API natürlich auf dem verwendeten PC installiert sein und es muss eine Verbindung zwischen dem PC und dem Funktionsgenerator bestehen.

# Write Waveform to Device
# Note: byte order = little-endian!
device.write_binary_values('C1:WVDT WVNM,STEREO_MPX,FREQ,100.0,TYPE,8,AMPL,1.0,OFST,0.0,PHASE,0.0,WAVEDATA,', WAVE, datatype='i', is_big_endian=False)

Das war’s! Das vollständige Python-Skript kann ebenfalls aus meinem GitHub-Repository heruntergeladen werden [2].

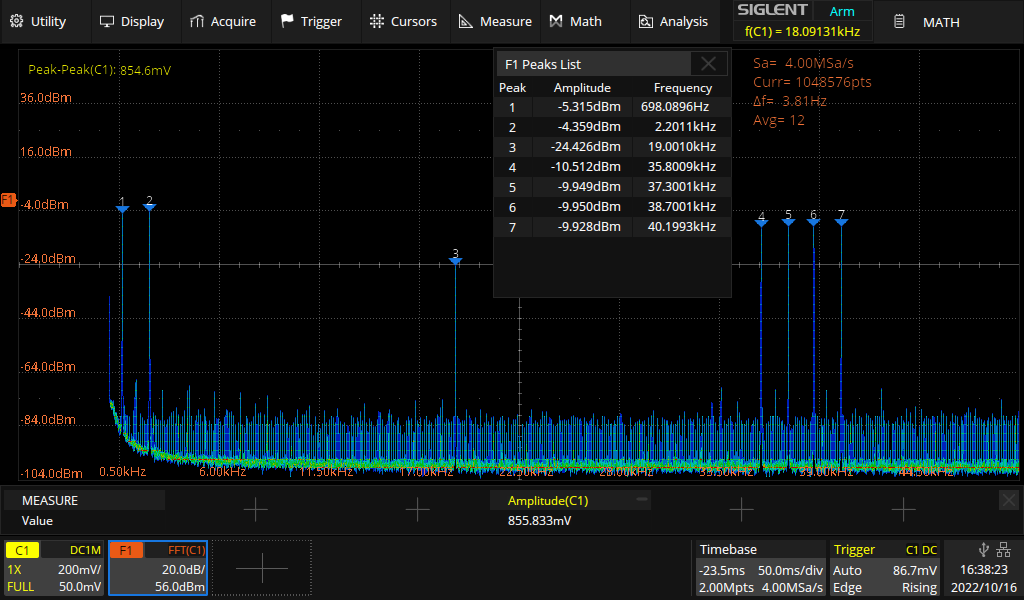
Nachdem das Python-Skript ausgeführt wurde, fing der Funktionsgenerator an das beabsichtigte Stereo-Multiplex-Signal zu erzeugen. Da hier nur 2 statische Audio-Töne für die beiden Audiokanäle erzeugt werden, können die Spektralanteile und die relativen Amplituden aller Signalbestandteile sehr gut im Spektrum beobachtet werden:

Spektrumdarstellung des Stereo-MPX-Signales

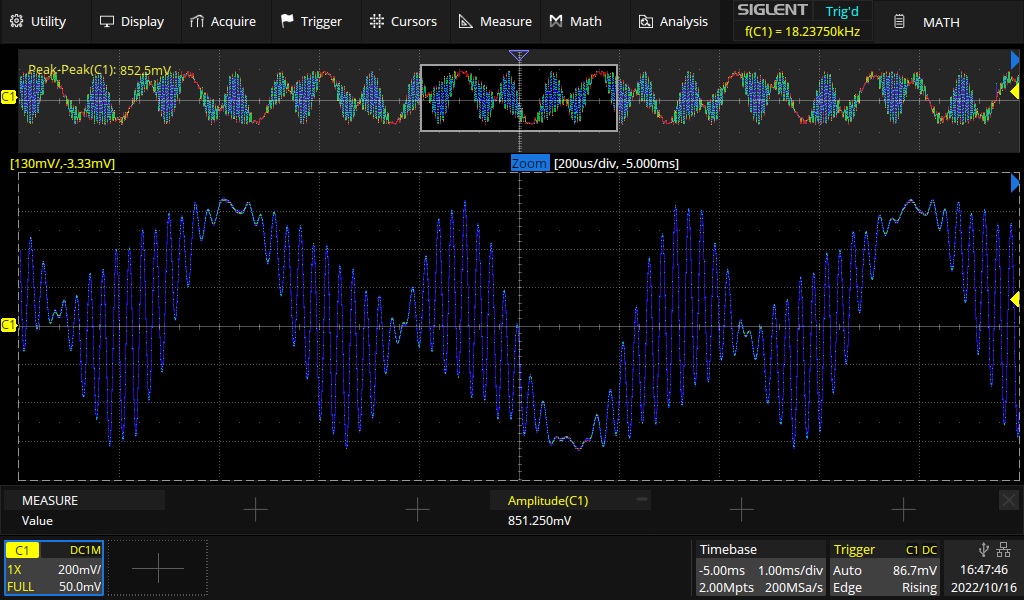
Der Vollständigkeit halber, hier das generierte Signal in der Zeitdomäne:

Generiertes Stereo-Multiplex-Signal in der Zeitdomäne

Im Kern kann gesagt werden, dass es sehr einfach ist mit Python Wellenformdaten für moderne Funktionsgeneratoren zu erzeugen. Solange eine mathematische Gleichung für die Wellenform aufgestellt werden kann, gibt es kaum Limits. Beim SDG1032X ist die größte Limitierung der relative kleine Samplespeicher mit nur 16384 Punkten. Nichtsdestotrotz, das hier zur Verfügung gestellte Python-Framework bietet eine gute Grundlage für das Erzeugen von komplexeren Wellenformen. Dazu muss lediglich die Zeile mit der mathematischen Beschreibung der Wellenform („WAVE[n] =“) angepasst werden. Mein GitHub-Repository enthält dazu weitere Beispiele.

Links und Quellen:

[1] BalticLab (2016): Stereo Multiplexing for FM Transmission | Theory

[2] AI5GW (2022): Python code examples for SIGLENT equipment